GPU Prefix Sum: From Multi-Kernel to Single-Pass Decoupled Lookback
Introduction
Prefix sum (scan) is a fundamental parallel primitive used in stream compaction, radix sort, and sparse matrix operations. Each output element depends on all elements before it, creating an inherent sequential dependency that makes efficient parallelization surprisingly difficult. The example below shows an inclusive scan:
\[\begin{aligned} \text{Input: } & [x_{0}, x_{1}, \ldots, x_{n-1}] \\ \text{Output: } & [x_{0}, (x_{0} + x_{1}), \ldots, (x_{0} + x_{1} + \ldots +x_{n-1})] \end{aligned}\]This post implements inclusive scan from first principles, progressively building toward the decoupled lookback algorithm used in production libraries like CUB. Rather than presenting the final solution upfront, we’ll develop each implementation and let benchmark results reveal what actually works and what doesn’t.
The benchmark code is available in this repository.
Block-Level Scan
Before tackling large arrays, we need an efficient way to scan within a single thread block. Figure 1 illustrates the Kogge-Stone parallel scan algorithm:
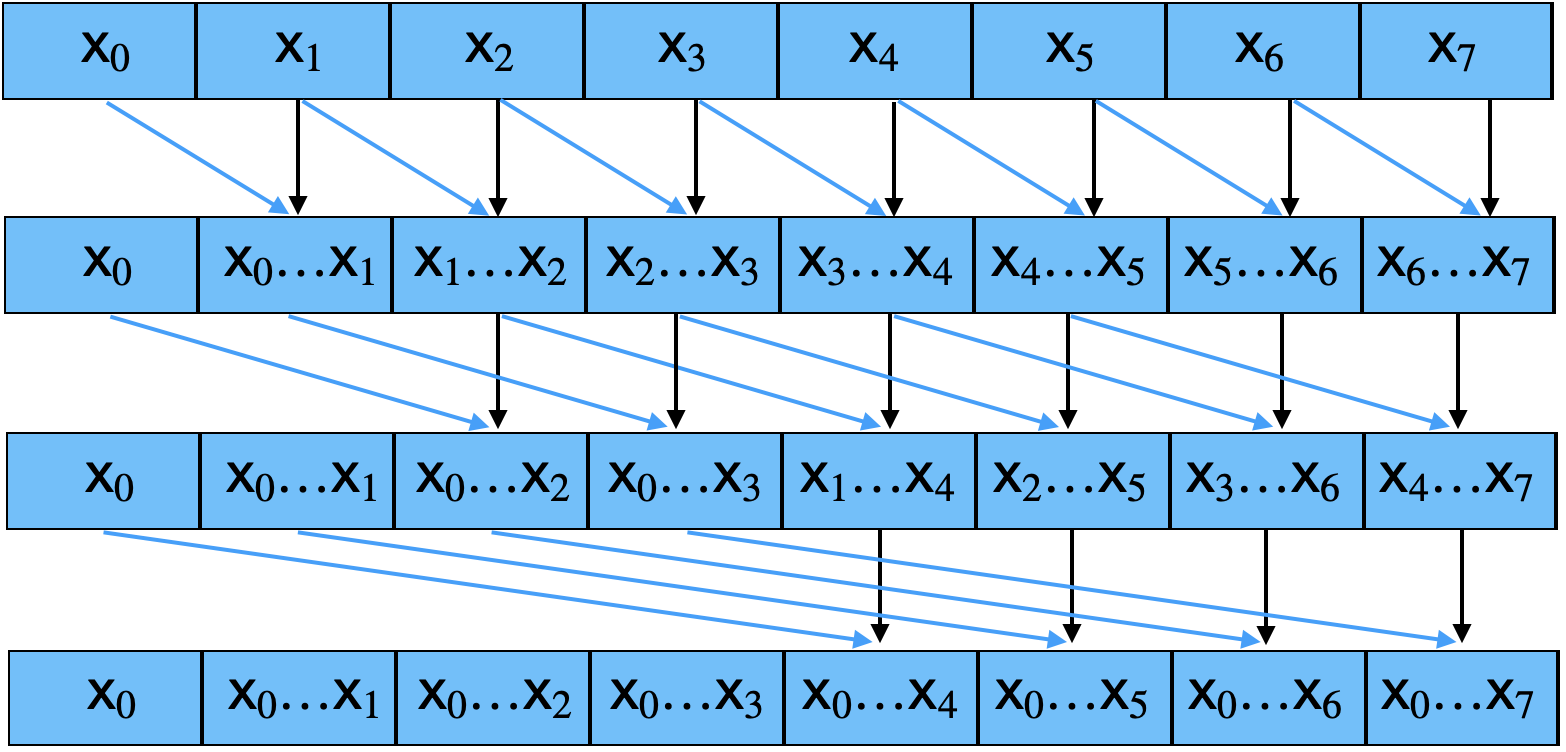
The algorithm proceeds in iterations. In the first iteration (offset = 1), each element adds its immediate left neighbor. In the second iteration (offset = 2), each element adds the element two positions to the left. After $\log_{2}(n)$ iterations, every position holds the prefix sum of all elements up to and including itself.
This approach is not work-efficient: it performs $O(n \log n)$ additions compared to the optimal $O(n)$. The Brent-Kung algorithm achieves $O(n)$ work by using a reduce-then-downsweep pattern. However, Kogge-Stone’s regular structure maps well to GPU warp primitives, and for this post I’ll use it to keep focus on multi-block optimization rather than block-level optimization complexities that come with the Brent-Kung algorithm. Besides, production libraries like CUB use the Kogge-Stone algorithm (as of the time of this writing).
Shared memory implementation
The simplest implementation of Kogge-Stone’s scan algorithm uses shared memory with double buffering to prevent race conditions. Each thread loads one element, then the block performs $\log_{2}(\text{BLOCK_SIZE})$ iterations:
template<int BLOCK_SIZE>
__global__ void ScanTilesSMEM(
const int* __restrict__ input,
int* __restrict__ output,
int n,
int* tile_aggregates)
{
const int gid = blockIdx.x * blockDim.x + threadIdx.x;
const int tid = threadIdx.x;
__shared__ int smem[2][BLOCK_SIZE];
int wbuf = 0;
smem[wbuf][tid] = (gid < n) ? input[gid] : 0;
__syncthreads();
for (int offset = 1; offset < BLOCK_SIZE; offset *= 2) {
wbuf = 1 - wbuf;
int rbuf = 1 - wbuf;
if (tid >= offset) {
smem[wbuf][tid] = smem[rbuf][tid - offset] + smem[rbuf][tid];
} else {
smem[wbuf][tid] = smem[rbuf][tid];
}
__syncthreads();
}
if (gid < n) {
output[gid] = smem[wbuf][tid];
}
if (tid == BLOCK_SIZE - 1 && tile_aggregates != nullptr) {
tile_aggregates[blockIdx.x] = smem[wbuf][BLOCK_SIZE - 1];
}
}
The double buffering alternates between two shared memory arrays: threads read from one buffer while writing to the other. With a 512-thread block, this requires 9 iterations ($\log_{2}(\text{BLOCK_SIZE})$), each with a __syncthreads() barrier. That’s substantial synchronization overhead, and the shared memory traffic adds up.
Warp shuffle optimization
Within a 32-thread warp, we can use shuffle intrinsics to exchange values directly between registers without touching shared memory:
static __device__ __forceinline__ int WarpScanInclusive(int value)
{
const int lane = threadIdx.x % warpSize;
#pragma unroll
for (int offset = 1; offset < warpSize; offset *= 2) {
int tmp = __shfl_up_sync(0xFFFFFFFF, value, offset);
if (lane >= offset) {
value += tmp;
}
}
return value;
}
The __shfl_up_sync instruction shifts values by offset lanes. For example, lane 5 receives the value from lane 4 when offset is 1, from lane 3 when offset is 2, and so on. After 5 iterations (since $2^{5} = 32$), each lane holds the inclusive scan of all preceding lanes. This happens entirely in registers, avoiding shared memory entirely.
However, a single warp only handles 32 elements. For a 512-thread block with 16 warps, we need a second level of hierarchy: scan within each warp, then scan across warp totals to compute the prefix each warp should add. This hierarchical scan idea to obtain block level scan is implemented below:
template<int BLOCK_SIZE>
static __device__ __forceinline__ int BlockScanInclusive(int value)
{
static_assert(BLOCK_SIZE % 32 == 0, "BLOCK_SIZE must be multiple of warp size");
const int warp_idx = threadIdx.x / warpSize;
const int lane = threadIdx.x % warpSize;
constexpr int NUM_WARPS = BLOCK_SIZE / 32;
// Step 1: Warp-level inclusive scan
int warp_scan = WarpScanInclusive(value);
// Step 2: Last lane of each warp writes its total to shared memory
__shared__ int warp_totals[NUM_WARPS];
if (lane == warpSize - 1) {
warp_totals[warp_idx] = warp_scan;
}
__syncthreads();
// Step 3: First warp scans the warp totals
if (warp_idx == 0) {
int warp_total = (lane < NUM_WARPS) ? warp_totals[lane] : 0;
warp_total = WarpScanInclusive(warp_total);
if (lane < NUM_WARPS) {
warp_totals[lane] = warp_total;
}
}
__syncthreads();
// Step 4: Add prefix from previous warps
int warp_prefix = (warp_idx > 0) ? warp_totals[warp_idx - 1] : 0;
return warp_scan + warp_prefix;
}
This two-level approach needs only NUM_WARPS elements of shared memory (16 for a 512-thread block) compared to $2 \times \text{BLOCK_SIZE}$ (1024) for double buffering, and requires just two __syncthreads() calls instead of nine. The tile scan kernel becomes straightforward:
template<int BLOCK_SIZE>
__global__ void ScanTilesWarp(
const int* __restrict__ input,
int* __restrict__ output,
int n,
int* tile_aggregates)
{
const int gid = blockIdx.x * blockDim.x + threadIdx.x;
int value = (gid < n) ? input[gid] : 0;
value = BlockScanInclusive<BLOCK_SIZE>(value);
if (gid < n) {
output[gid] = value;
}
if (threadIdx.x == BLOCK_SIZE - 1 && tile_aggregates != nullptr) {
tile_aggregates[blockIdx.x] = value;
}
}
Scaling Beyond a Single Block
A single thread block can process at most around 1024 elements (limited by maximum threads per block). For over a billion elements, we need to coordinate across millions of blocks. Figure 2 illustrates the standard reduce-then-scan approach:
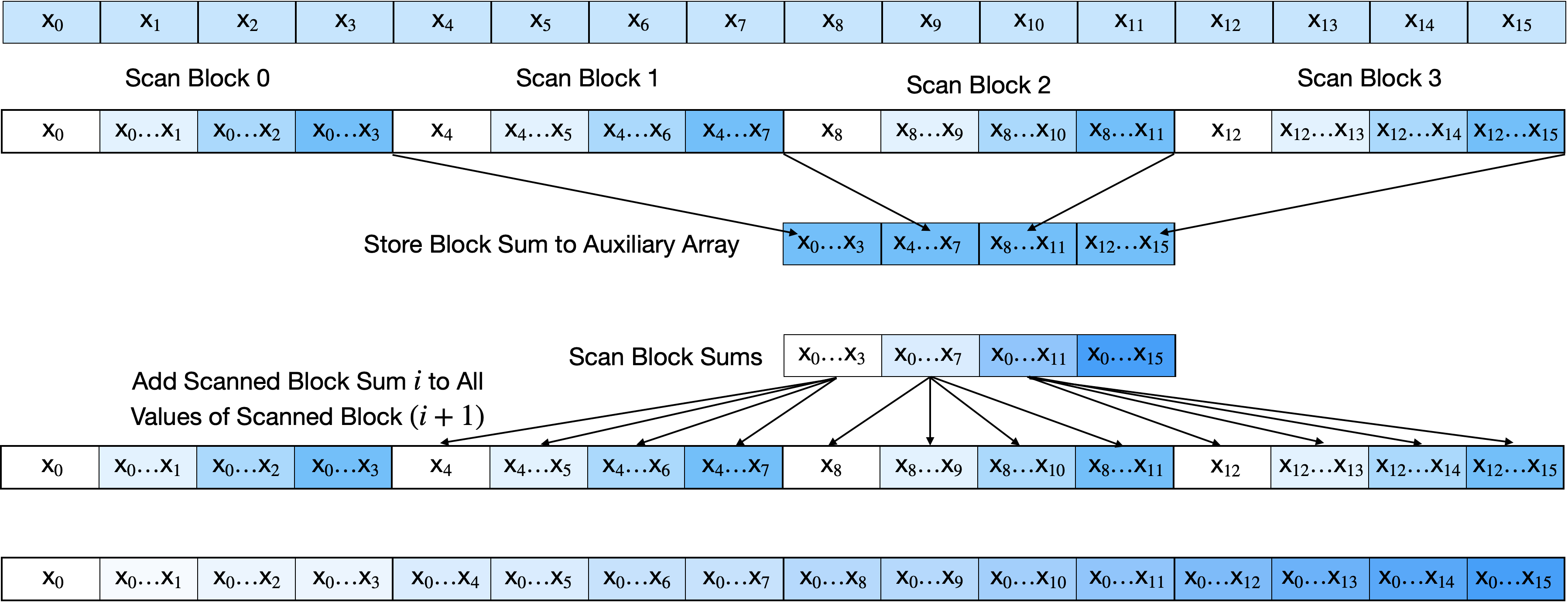
The algorithm has three phases:
-
Scan tiles independently: Each block scans its local elements and writes its final sum (the tile aggregate) to an auxiliary array.
-
Scan the aggregates: The auxiliary array of tile sums is itself scanned, either with a single block (if small enough) or recursively using the same three-phase approach.
-
Propagate prefixes: Each block adds the scanned aggregate of the previous tile to all its elements, completing the global scan.
For an input array of $2^{30}$ elements and a tile size of 512 ($2^9$), the initial scan produces $2^{21}$ tiles. Recursively scanning the auxiliary arrays gives the sequence $2^{21} \rightarrow 2^{12} \rightarrow 2^3 \rightarrow 1$. Accounting for both the scan and prefix-propagation kernels at each level, this requires at least 6 kernel launches.
To keep this post focused on the kernels only, I will not show the host codes for launching the kernels. Interested readers are directed to the repository.
Baseline results
All benchmarks in this post use an H100 (3352.32 GB/s peak bandwidth) with $2^{30}$ int elements:
| Kernel | Time (ms) | Bandwidth | % Peak |
|---|---|---|---|
| Multi-kernel (SMEM) | 10.72 | 801.52 GB/s | 23.9% |
| Multi-kernel (Warp shuffle) | 9.33 | 920.52 GB/s | 27.5% |
The warp shuffle version is about 15% faster, but both are well below peak bandwidth. Multiple kernel launches and the hierarchical structure leave performance on the table. Can we do better with a single-pass approach?
The Single-Pass Challenge
The multi-kernel approach works, but each kernel launch carries overhead: queue submission, SM scheduling, and synchronization. With recursive launches for large arrays, this adds up. A single kernel that processes all tiles would eliminate this overhead entirely.
The obvious approach is to have each tile wait for the previous tile to finish, grab its prefix, add it to local results, then publish its own prefix for the next tile. But there’s a fundamental problem: CUDA provides no guarantees about block scheduling order.
The solution is to decouple logical tile order from physical block IDs. Each block atomically claims a logical tile index at runtime, ensuring that tiles are processed in the order blocks happen to execute:
__shared__ int s_tile_idx;
if (threadIdx.x == 0) {
s_tile_idx = atomicAdd(g_tile_counter, 1);
}
__syncthreads();
const int tile_idx = s_tile_idx; // Logical tile index, not blockIdx.x
With dynamic indexing, tiles that run earlier get lower indices, so spin-waiting for a predecessor is safe since that predecessor is guaranteed to have already started executing.
Chained Scan: First Attempt
Armed with dynamic tile indexing, let’s try the straightforward single-pass approach. Each tile scans locally, waits for its predecessor to publish a prefix, adds that prefix, then publishes its own:
template<int BLOCK_SIZE>
__global__ void ScanChainedKernel(
const int* __restrict__ input,
int* __restrict__ output,
int n,
int* tile_prefixes,
int* tile_ready,
int* g_tile_counter)
{
__shared__ int s_tile_idx;
__shared__ int s_prefix;
// Step 1: Dynamically claim logical tile index
if (threadIdx.x == 0) {
s_tile_idx = atomicAdd(g_tile_counter, 1);
}
__syncthreads();
const int tile_idx = s_tile_idx;
const int gid = tile_idx * BLOCK_SIZE + threadIdx.x;
// Step 2: Load and scan tile
int value = (gid < n) ? input[gid] : 0;
value = BlockScanInclusive<BLOCK_SIZE>(value);
// Step 3: Single thread handles inter-tile communication
if (threadIdx.x == BLOCK_SIZE - 1) {
if (tile_idx == 0) {
// First tile: no predecessor to wait for
s_prefix = 0;
} else {
// Spin-wait for previous tile to be ready
while (atomicAdd(&tile_ready[tile_idx - 1], 0) == 0) {
// Spin
}
s_prefix = tile_prefixes[tile_idx - 1];
}
// Publish our prefix (previous prefix + our tile total)
tile_prefixes[tile_idx] = s_prefix + value;
__threadfence(); // Ensure prefix visible BEFORE ready flag
atomicExch(&tile_ready[tile_idx], 1);
}
__syncthreads();
// Step 4: All threads add prefix and write output
if (gid < n) {
output[gid] = s_prefix + value;
}
}
The chained scan uses a single kernel, no recursive launches, and simple logic. Let’s check the benchmark:
| Kernel | Time (ms) | Bandwidth | % Peak |
|---|---|---|---|
| Multi-kernel (SMEM) | 10.72 | 801.52 GB/s | 23.9% |
| Multi-kernel (Warp shuffle) | 9.33 | 920.52 GB/s | 27.5% |
| Chained scan | 1767.29 | 4.86 GB/s | 0.14% |
That’s not a typo. 0.14% of peak bandwidth. What went wrong?
The problem is serialization. Although all tiles launch in parallel and perform their local scans concurrently, the algorithm imposes a strict dependency chain between tiles. Each tile must wait for tile $i - 1$ to publish its inclusive prefix before it can add that prefix to its local scan results, compute its own inclusive prefix, and make it visible to the next tile. This turns the inter-tile prefix propagation into a serialized critical path, effectively negating global parallelism.
Decoupled Lookback: Breaking the Chain
The chained scan’s fatal flaw is that tiles wait for complete prefix information before they can finish. The decoupled lookback algorithm, introduced by Merrill and Garland (2016), breaks this dependency by publishing partial information immediately.
The key insight is that a tile can publish its local aggregate (the sum of just its elements) right after scanning, without waiting for any predecessor. Later tiles can use this partial information while looking backward for a complete prefix.
Three-state protocol
Each tile’s status progresses through three states:
INVALID -> Tile hasn't finished scanning yet
AGGREGATE -> Tile has published its local sum (no predecessor info)
PREFIX -> Tile has published its complete prefix (usable directly)
We pack both the value and status into a single 8-byte structure, allowing atomic updates to both fields simultaneously:
enum class TileStatus : int {
INVALID = 0,
AGGREGATE = 1,
PREFIX = 2
};
union TileDescriptor {
unsigned long long int raw; // For atomic operations
struct {
int value; // Aggregate or prefix sum
TileStatus status; // Current tile state
};
};
static_assert(sizeof(TileDescriptor) == 8, "TileDescriptor must be 8 bytes for atomic ops");
Why a union instead of two separate arrays? Consider what happens with separate arrays: a reader might see the updated status (AGGREGATE) but read a stale value (0) if those two writes become visible in different orders. The 64-bit atomic ensures both fields are read and written together, eliminating this race condition.
The algorithm
Instead of waiting before publishing, tiles publish their AGGREGATE immediately after scanning:
Decoupled (parallel):
Tile 0: [scan]--[PREFIX]
Tile 1: [scan]--[AGGREGATE]--[lookback]--[PREFIX]
Tile 2: [scan]--[AGGREGATE]------[lookback]--[PREFIX]
Tile 3: [scan]--[AGGREGATE]----------[lookback]--[PREFIX]
| tiles publish AGGREGATE immediately, then look backward
The lookback phase walks backward through predecessor tiles, accumulating values. When it encounters an AGGREGATE, it adds the value and continues backward. When it encounters a PREFIX, it adds the value and stops because that prefix already includes all earlier tiles. The accumulated sum becomes this tile’s exclusive prefix, which it combines with its local aggregate and publishes as PREFIX for later tiles to use.
Single-thread lookback implementation
A simple implementation of the decoupled lookback elects a single thread in a block to do the lookback:
template<int BLOCK_SIZE>
__global__ void ScanLookbackSingleThreadKernel(
const int* __restrict__ input,
int* __restrict__ output,
int n,
TileDescriptor* tile_descriptors,
int* g_tile_counter)
{
__shared__ int s_tile_idx;
__shared__ int s_tile_aggregate;
__shared__ int s_prefix;
// Step 1: Claim tile index
if (threadIdx.x == 0) {
s_tile_idx = atomicAdd(g_tile_counter, 1);
}
__syncthreads();
const int tile_idx = s_tile_idx;
const int gid = tile_idx * BLOCK_SIZE + threadIdx.x;
// Step 2: Load and scan tile
int value = (gid < n) ? input[gid] : 0;
value = BlockScanInclusive<BLOCK_SIZE>(value);
// Last thread writes aggregate to shared memory
if (threadIdx.x == BLOCK_SIZE - 1) {
s_tile_aggregate = value;
}
__syncthreads();
// Step 3: Thread 0 does the decoupled lookback
if (threadIdx.x == 0) {
const int tile_aggregate = s_tile_aggregate;
// Publish aggregate immediately (don't wait!)
TileDescriptor my_info;
my_info.value = tile_aggregate;
my_info.status = (tile_idx == 0) ? TileStatus::PREFIX : TileStatus::AGGREGATE;
atomicExch(&tile_descriptors[tile_idx].raw, my_info.raw);
__threadfence();
if (tile_idx == 0) {
s_prefix = 0;
} else {
int lookback_idx = tile_idx - 1;
int running_prefix = 0;
// Lookback loop: walk backward until we find PREFIX
while (lookback_idx >= 0) {
TileDescriptor pred_info;
// Spin-wait for valid data
do {
pred_info.raw = atomicAdd(&tile_descriptors[lookback_idx].raw, 0);
} while (pred_info.status == TileStatus::INVALID);
running_prefix += pred_info.value;
if (pred_info.status == TileStatus::PREFIX) {
break;
}
lookback_idx--;
}
s_prefix = running_prefix;
// Upgrade to PREFIX
my_info.value = running_prefix + tile_aggregate;
my_info.status = TileStatus::PREFIX;
atomicExch(&tile_descriptors[tile_idx].raw, my_info.raw);
__threadfence();
}
}
__syncthreads();
// Step 4: All threads add prefix and write
if (gid < n) {
output[gid] = s_prefix + value;
}
}
The critical difference from chained scan is timing. Chained scan waits for the predecessor’s complete PREFIX before doing anything useful. Decoupled lookback publishes its AGGREGATE immediately, then looks backward and accumulates whatever information is available, whether PREFIX or AGGREGATE. Tiles that finish their lookback early produce PREFIXes that short-circuit the search for everyone behind them.
| Kernel | Time (ms) | Bandwidth | % Peak |
|---|---|---|---|
| Multi-kernel (SMEM) | 10.72 | 801.52 GB/s | 23.9% |
| Multi-kernel (Warp shuffle) | 9.33 | 920.52 GB/s | 27.5% |
| Chained scan | 1767.29 | 4.86 GB/s | 0.14% |
| Single-thread lookback | 34.34 | 250.17 GB/s | 7.5% |
That’s an improvement over chained scan and the algorithm works. But it’s still slower than the multi-kernel baseline. The lookback loop is the culprit: one thread serially walks through potentially many predecessor tiles, issuing atomic reads one at a time.
Warp-Level Lookback
The single-thread bottleneck has an obvious fix: parallelize the lookback across multiple threads. A warp has 32 threads that execute in lockstep, perfect for checking 32 predecessor tiles simultaneously:
Warp lookback pattern (tile 1000 needs its prefix):
Iteration 1: lanes 0-31 check tiles 999, 998, ..., 968 in parallel
-> All return AGGREGATE
-> Sum all 32 values, continue backward
Iteration 2: lanes 0-31 check tiles 967, 966, ..., 936 in parallel
-> Lane 5 finds tile 962 = PREFIX
-> Sum lanes 0-5 only, add to running total, done
The implementation uses three warp primitives to coordinate the parallel search:
__ballot_sync(): Returns a 32-bit mask indicating which lanes found a PREFIX__ffs(): Finds the first (lowest) set bit, giving the PREFIX closest to our tile__shfl_xor_sync: Sums contributions across lanes in $O(\log_{2} 32) = 5$ steps
template<int BLOCK_SIZE>
__global__ void ScanLookbackWarpKernel(
const int* __restrict__ input,
int* __restrict__ output,
int n,
TileDescriptor* tile_descriptors,
int* g_tile_counter)
{
__shared__ int s_tile_idx;
__shared__ int s_tile_aggregate;
__shared__ int s_prefix;
// Step 1: Claim tile index
if (threadIdx.x == 0) {
s_tile_idx = atomicAdd(g_tile_counter, 1);
}
__syncthreads();
const int tile_idx = s_tile_idx;
const int gid = tile_idx * BLOCK_SIZE + threadIdx.x;
// Step 2: Load and scan tile
int value = (gid < n) ? input[gid] : 0;
value = BlockScanInclusive<BLOCK_SIZE>(value);
// Last thread writes aggregate to shared memory
if (threadIdx.x == BLOCK_SIZE - 1) {
s_tile_aggregate = value;
}
__syncthreads();
// Step 3: Warp 0 does the decoupled lookback
const int warp_idx = threadIdx.x / warpSize;
const int lane = threadIdx.x % warpSize;
if (warp_idx == 0) {
const int tile_aggregate = s_tile_aggregate;
// Publish aggregate (thread 0 writes)
if (threadIdx.x == 0) {
TileDescriptor my_info;
my_info.value = tile_aggregate;
my_info.status = (tile_idx == 0) ? TileStatus::PREFIX : TileStatus::AGGREGATE;
atomicExch(&tile_descriptors[tile_idx].raw, my_info.raw);
__threadfence();
}
__syncwarp();
if (tile_idx == 0) {
if (threadIdx.x == 0) {
s_prefix = 0;
}
} else {
int exclusive_prefix = 0;
int lookback_base = tile_idx - 1;
while (true) {
// Each lane checks a different predecessor
const int my_lookback_idx = lookback_base - lane;
TileDescriptor pred_info;
pred_info.value = 0;
pred_info.status = TileStatus::PREFIX; // Default for out-of-bounds
if (my_lookback_idx >= 0) {
do {
pred_info.raw = atomicAdd(&tile_descriptors[my_lookback_idx].raw, 0);
} while (pred_info.status == TileStatus::INVALID);
}
// Find which lanes found PREFIX
const unsigned prefix_mask = __ballot_sync(0xFFFFFFFF,
pred_info.status == TileStatus::PREFIX);
const int prefix_lane = __ffs(prefix_mask) - 1; // -1 if none found
// Include all lanes if no PREFIX found, otherwise lanes 0..prefix_lane
int contribution = (prefix_lane < 0 || lane <= prefix_lane) ? pred_info.value : 0;
// XOR reduction - all lanes get the sum
#pragma unroll
for (int offset = warpSize / 2; offset > 0; offset /= 2) {
contribution += __shfl_xor_sync(0xFFFFFFFF, contribution, offset);
}
exclusive_prefix += contribution;
// If we found any PREFIX, we're done
if (prefix_lane >= 0) {
break;
}
// All 32 were AGGREGATE, continue to earlier tiles
lookback_base -= warpSize;
}
// Thread 0 writes prefix to shared memory
if (threadIdx.x == 0) {
s_prefix = exclusive_prefix;
// Upgrade to PREFIX
TileDescriptor my_info;
my_info.value = exclusive_prefix + tile_aggregate;
my_info.status = TileStatus::PREFIX;
atomicExch(&tile_descriptors[tile_idx].raw, my_info.raw);
__threadfence();
}
}
}
__syncthreads();
// Step 4: All threads add prefix and write
if (gid < n) {
output[gid] = s_prefix + value;
}
}
The XOR reduction deserves explanation. After each lane loads its predecessor’s value, we need the sum of lanes 0 through prefix_lane. The __shfl_xor_sync instruction performs an iterative all-reduce. Lanes beyond prefix_lane are masked out before the reduction by setting their contributions to zero.
Adding to the tally:
| Kernel | Time (ms) | Bandwidth | % Peak |
|---|---|---|---|
| Multi-kernel (SMEM) | 10.72 | 801.52 GB/s | 23.9% |
| Multi-kernel (Warp shuffle) | 9.33 | 920.52 GB/s | 27.5% |
| Chained scan | 1767.29 | 4.86 GB/s | 0.14% |
| Single-thread lookback | 34.34 | 250.17 GB/s | 7.5% |
| Warp lookback | 15.06 | 570.55 GB/s | 17.0% |
From the table, we see an improvement over single-thread, but we’re still slower than multi-kernel.
Coarsening and Vectorization: The Missing Piece
The technique combines two optimizations: thread coarsening (each thread processes multiple elements) and vectorized loads (using 128-bit int4 loads for better memory bandwidth). For example, a 512-thread block where each thread loads three int4 vectors handles $512 \times 3 \times 4 = 6144$ elements per tile.
This structure adds a third level to our scan hierarchy: each thread first scans its own elements locally, then the block scans across thread totals using an exclusive scan (so each thread gets the sum of all preceding threads’ elements). This mirrors the warp-then-block pattern, now extended to thread-then-warp-then-block.
A key detail is the data layout. Vectorized loads want a striped access pattern where consecutive threads access consecutive int4 vectors (coalesced memory access). But the local scan wants a blocked layout where each thread’s elements are contiguous in memory. The solution is to transpose between these layouts using shared memory.
The full implementation of the kernel is shown below:
template<int BLOCK_SIZE, int VEC_LOADS>
__global__ void ScanLookbackWarpCoarsenedVectorizedKernel(
const int* __restrict__ input,
int* __restrict__ output,
int n,
TileDescriptor* tile_descriptors,
int* g_tile_counter)
{
constexpr int ITEMS_PER_THREAD = VEC_LOADS * 4;
constexpr int TILE_SIZE = BLOCK_SIZE * ITEMS_PER_THREAD;
__shared__ int s_tile_idx;
__shared__ int s_tile_aggregate;
__shared__ int s_prefix;
__shared__ int s_exchange[TILE_SIZE];
// Step 1: Claim tile index
if (threadIdx.x == 0) {
s_tile_idx = atomicAdd(g_tile_counter, 1);
}
__syncthreads();
const int tile_idx = s_tile_idx;
const int tile_offset = tile_idx * TILE_SIZE;
// Step 2: Load using int4 with STRIPED access pattern (coalesced)
int items[ITEMS_PER_THREAD];
const int4* input_vec = reinterpret_cast<const int4*>(input + tile_offset);
#pragma unroll
for (int v = 0; v < VEC_LOADS; v++) {
const int vec_idx = threadIdx.x + v * BLOCK_SIZE;
const int base_idx = tile_offset + vec_idx * 4;
if (base_idx + 3 < n) {
int4 loaded = input_vec[vec_idx];
items[v * 4 + 0] = loaded.x;
items[v * 4 + 1] = loaded.y;
items[v * 4 + 2] = loaded.z;
items[v * 4 + 3] = loaded.w;
} else {
#pragma unroll
for (int i = 0; i < 4; i++) {
const int idx = base_idx + i;
items[v * 4 + i] = (idx < n) ? input[idx] : 0;
}
}
}
// Step 3: Transpose STRIPED -> BLOCKED via shared memory
#pragma unroll
for (int v = 0; v < VEC_LOADS; v++) {
const int smem_idx = (threadIdx.x + v * BLOCK_SIZE) * 4;
s_exchange[smem_idx + 0] = items[v * 4 + 0];
s_exchange[smem_idx + 1] = items[v * 4 + 1];
s_exchange[smem_idx + 2] = items[v * 4 + 2];
s_exchange[smem_idx + 3] = items[v * 4 + 3];
}
__syncthreads();
#pragma unroll
for (int i = 0; i < ITEMS_PER_THREAD; i++) {
items[i] = s_exchange[threadIdx.x * ITEMS_PER_THREAD + i];
}
__syncthreads();
// Step 4: Thread-local inclusive scan (blocked layout)
#pragma unroll
for (int i = 1; i < ITEMS_PER_THREAD; i++) {
items[i] += items[i - 1];
}
// Step 5: BlockScan on thread totals (exclusive)
const int thread_total = items[ITEMS_PER_THREAD - 1];
const int thread_prefix = BlockScanExclusive<BLOCK_SIZE>(thread_total);
// Step 6: Add thread prefix to all items
#pragma unroll
for (int i = 0; i < ITEMS_PER_THREAD; i++) {
items[i] += thread_prefix;
}
// Last thread writes tile aggregate to shared memory
if (threadIdx.x == BLOCK_SIZE - 1) {
s_tile_aggregate = items[ITEMS_PER_THREAD - 1];
}
__syncthreads();
// Step 7: Warp 0 does the decoupled lookback
// ... [warp lookback code identical to previous kernel] ...
// Step 8: Add global prefix to all items
#pragma unroll
for (int i = 0; i < ITEMS_PER_THREAD; i++) {
items[i] += s_prefix;
}
// Step 9: Transpose BLOCKED -> STRIPED via shared memory
#pragma unroll
for (int i = 0; i < ITEMS_PER_THREAD; i++) {
s_exchange[threadIdx.x * ITEMS_PER_THREAD + i] = items[i];
}
__syncthreads();
#pragma unroll
for (int v = 0; v < VEC_LOADS; v++) {
const int smem_idx = (threadIdx.x + v * BLOCK_SIZE) * 4;
items[v * 4 + 0] = s_exchange[smem_idx + 0];
items[v * 4 + 1] = s_exchange[smem_idx + 1];
items[v * 4 + 2] = s_exchange[smem_idx + 2];
items[v * 4 + 3] = s_exchange[smem_idx + 3];
}
__syncthreads();
// Step 10: Store using int4 with STRIPED access pattern (coalesced)
int4* output_vec = reinterpret_cast<int4*>(output + tile_offset);
#pragma unroll
for (int v = 0; v < VEC_LOADS; v++) {
const int vec_idx = threadIdx.x + v * BLOCK_SIZE;
const int base_idx = tile_offset + vec_idx * 4;
if (base_idx + 3 < n) {
int4 result;
result.x = items[v * 4 + 0];
result.y = items[v * 4 + 1];
result.z = items[v * 4 + 2];
result.w = items[v * 4 + 3];
output_vec[vec_idx] = result;
} else {
#pragma unroll
for (int i = 0; i < 4; i++) {
const int idx = base_idx + i;
if (idx < n) {
output[idx] = items[v * 4 + i];
}
}
}
}
}
Sweeping through different coarsening factors and adding CUB’s DeviceScan implementation for comparison:
| Kernel | Time (ms) | Bandwidth | % Peak |
|---|---|---|---|
| Multi-kernel (SMEM) | 10.72 | 801.52 GB/s | 23.9% |
| Multi-kernel (Warp shuffle) | 9.33 | 920.52 GB/s | 27.5% |
| Chained scan | 1767.29 | 4.86 GB/s | 0.14% |
| Single-thread lookback | 34.34 | 250.17 GB/s | 7.5% |
| Warp lookback | 15.06 | 570.55 GB/s | 17.0% |
| Coarsened + vec ($\times$4 elems/thread) | 5.29 | 1624.18 GB/s | 48.4% |
| Coarsened + vec ($\times$8 elems/thread) | 4.75 | 1807.59 GB/s | 53.9% |
| Coarsened + vec ($\times$12 elems/thread) | 3.44 | 2495.06 GB/s | 74.4% |
| Coarsened + vec ($\times$16 elems/thread) | 6.28 | 1366.81 GB/s | 40.8% |
| CUB DeviceScan | 3.47 | 2478.55 GB/s | 73.9% |
Processing 12 elements per thread produces the best result, getting us to 74.4% of peak bandwidth, which matches the production-grade implementation in CUB.
Conclusion
Building an efficient single-pass scan requires solving multiple problems together.
Dynamic tile indexing decouples logical order from hardware scheduling, making spin-waits safe without risking deadlock.
The three-state protocol (INVALID, AGGREGATE, PREFIX) allows tiles to publish partial information immediately. This is the key insight that breaks the serialization chain: tiles don’t wait for complete prefixes before contributing their local results.
Decoupled lookback lets tiles scan in parallel and look backward for whatever prefix information is available. Early PREFIXes propagate forward through the tile sequence, short-circuiting the search for later tiles.
Warp-level parallelism accelerates the lookback phase by checking 32 predecessors simultaneously, reducing iteration count by up to $32\times$.
Coarsening and vectorization reduce tile count while improving memory bandwidth utilization. This turns out to be critical: without larger tiles, lookback overhead dominates and single-pass actually loses to the multi-kernel approach.